Diffusion Schrodinger Bridge
Published:
A novel interpretation of diffusion based generative modeling, extending beyond the first time reversal, enabling faster generative models and dataset interpolation / unpaired image to image translation. Accepted as a spotlight paper at NeurIPS 2021.
Paper: https://arxiv.org/abs/2106.01357
Cite
``` @article{de2021diffusion, title={Diffusion Schr{\"o}dinger bridge with applications to score-based generative modeling}, author={De Bortoli, Valentin and Thornton, James and Heng, Jeremy and Doucet, Arnaud}, journal={Advances in Neural Information Processing Systems}, volume={34}, pages={17695--17709}, year={2021} } ```Contributors
Valentin De Bortoli, James Thornton, Jeremy Heng, Arnaud Doucet
What is a Schrödinger bridge?
The Schrödinger Bridge (SB) problem is a classical problem appearing in applied mathematics, optimal control and probability; see [1, 2, 3]. In the discrete-time setting, it takes the following (dynamic) form. Consider as reference density p(x0:N) describing the process adding noise to the data. We aim to find p*(x0:N) such that p*(x0) = pdata(x0) and p*(xN) = pprior(xN) and minimize the Kullback-Leibler divergence between p* and p. In this work we introduce Diffusion Schrodinger Bridge (DSB), a new algorithm which uses score-matching approaches [4] to approximate the Iterative Proportional Fitting algorithm, an iterative method to find the solutions of the SB problem. DSB can be seen as a refinement of existing score-based generative modeling methods [5, 6].
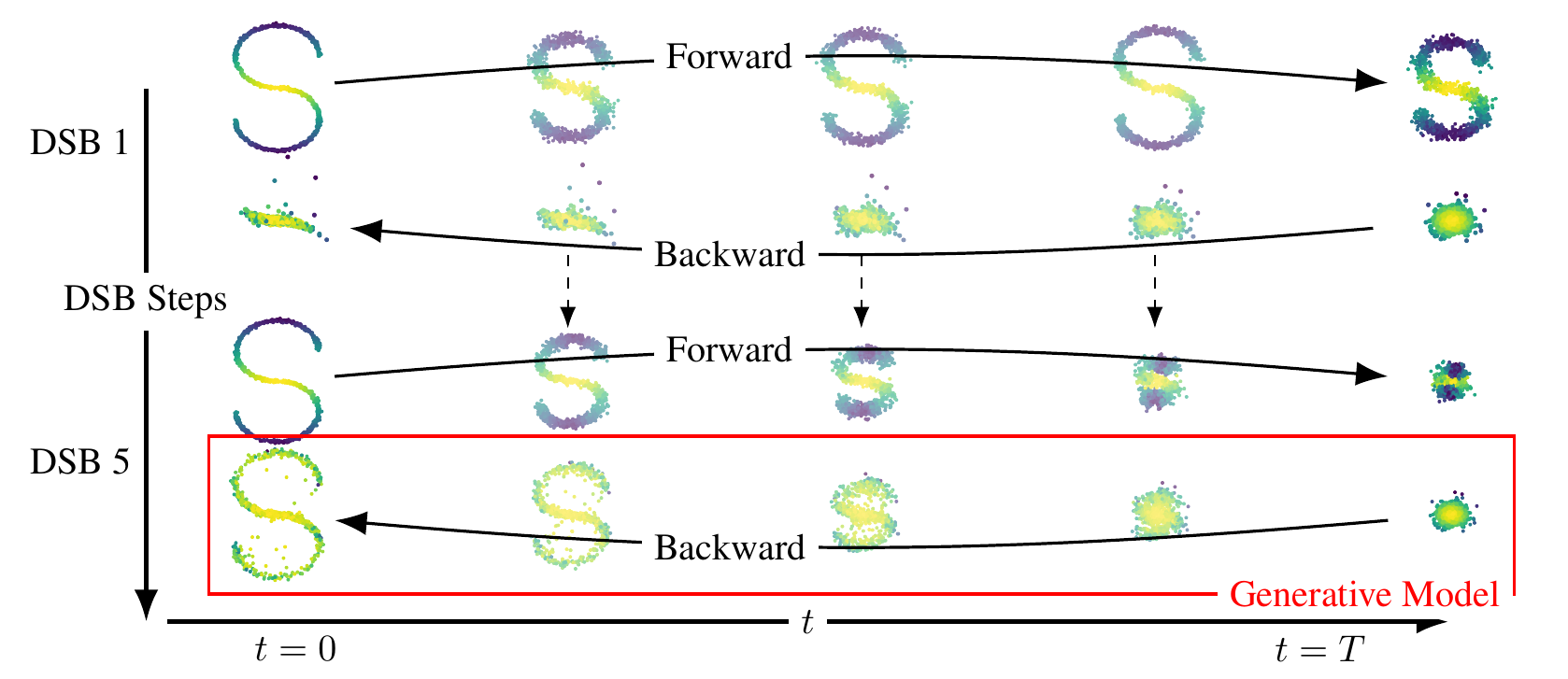
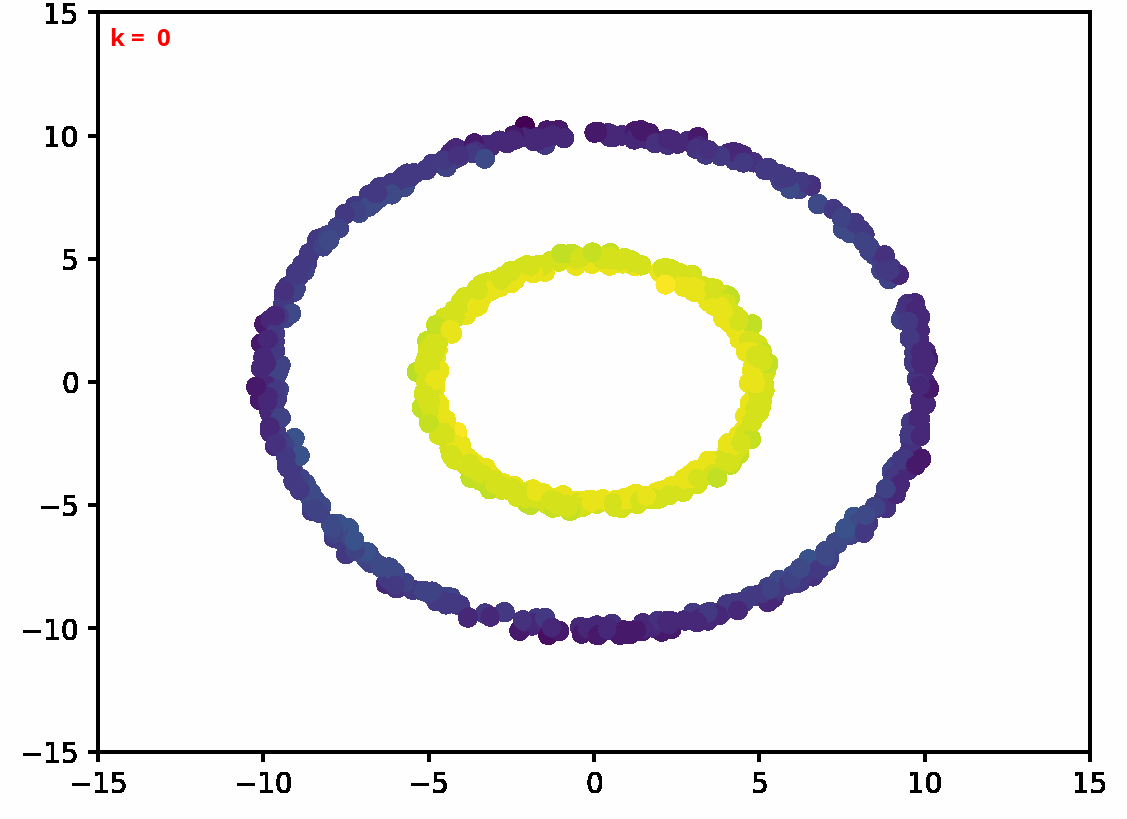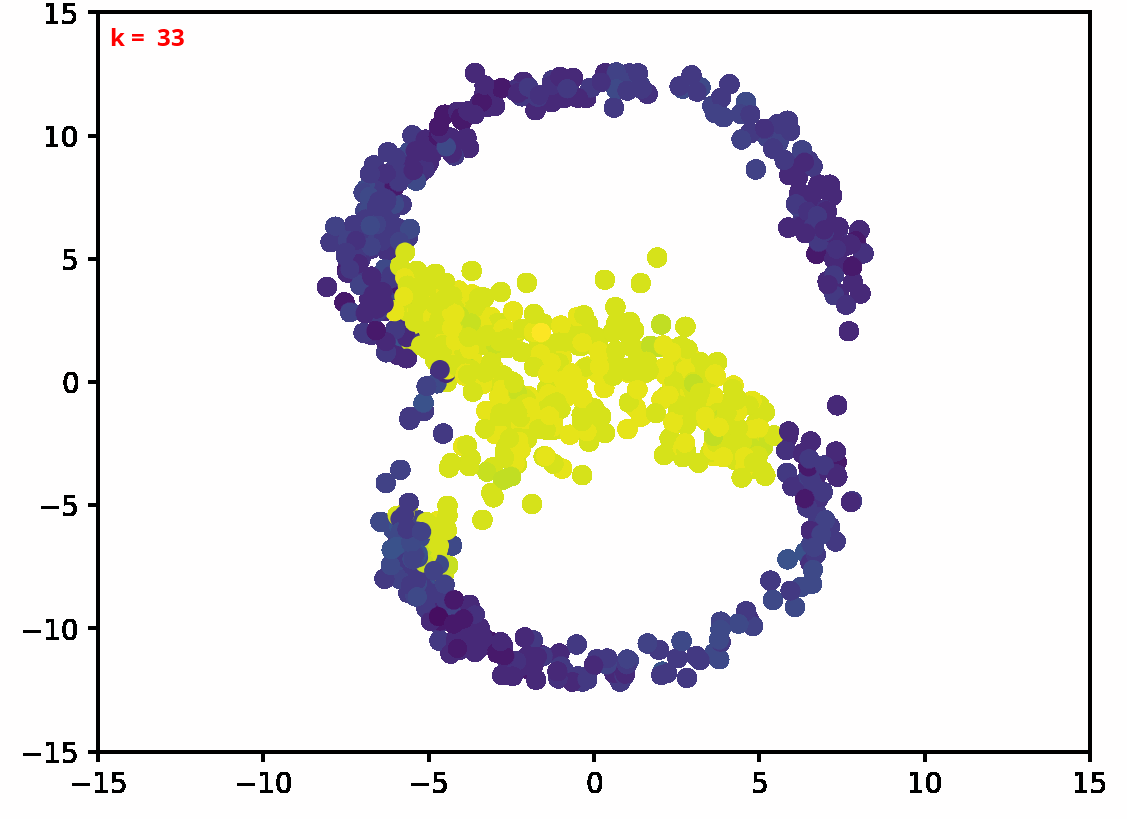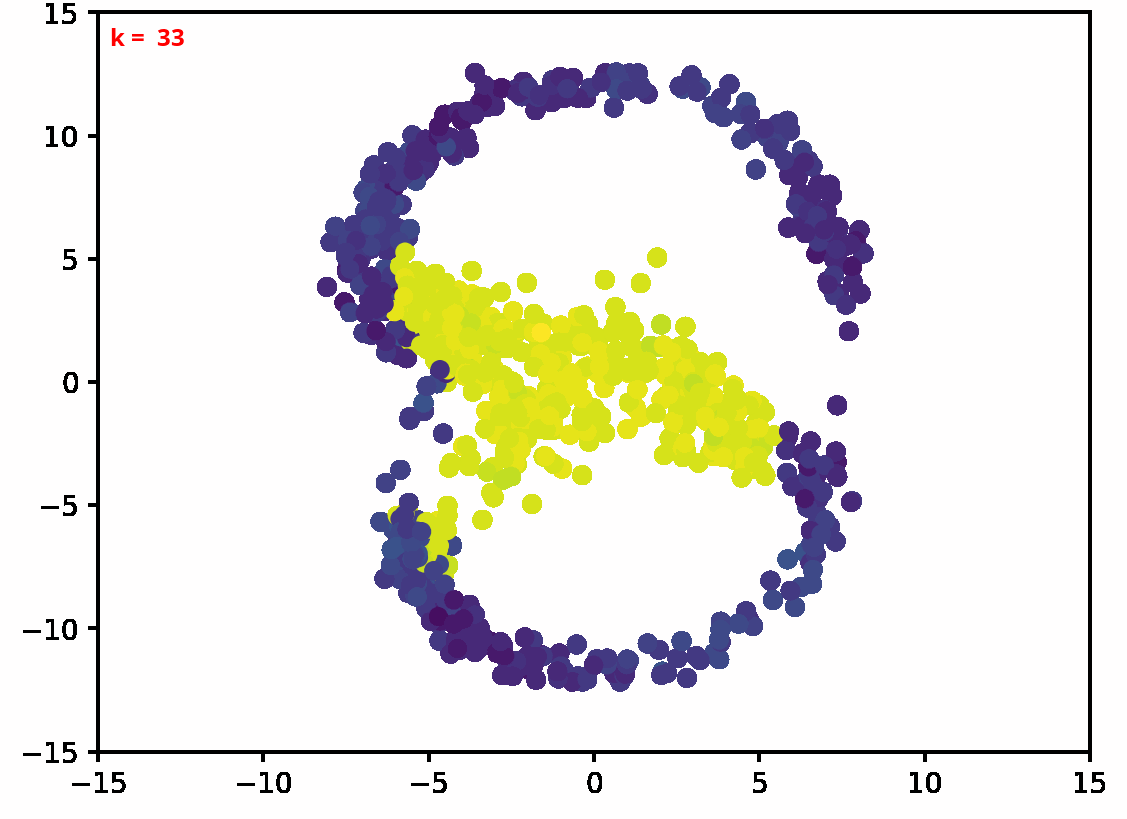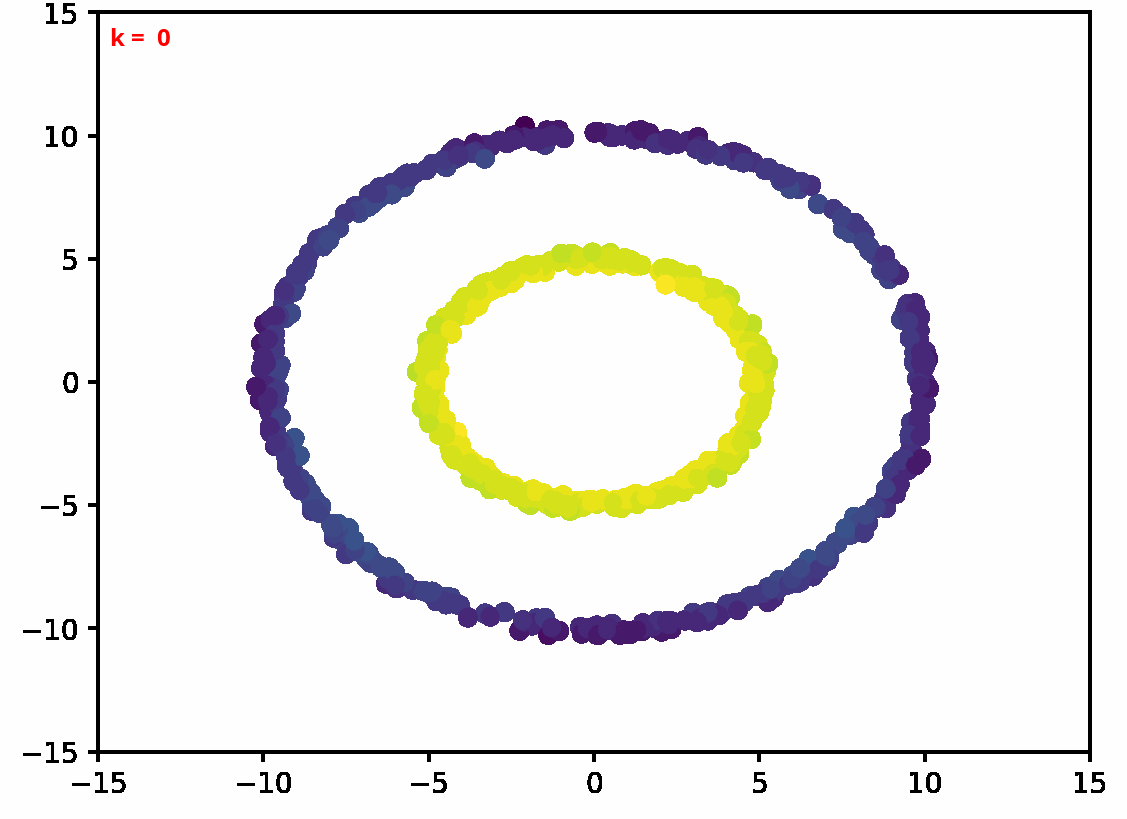
Two dimensional examples


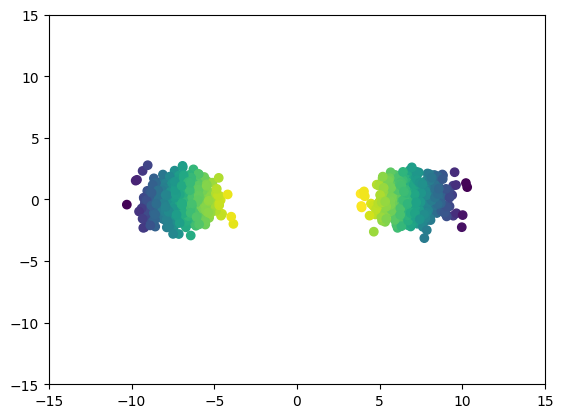
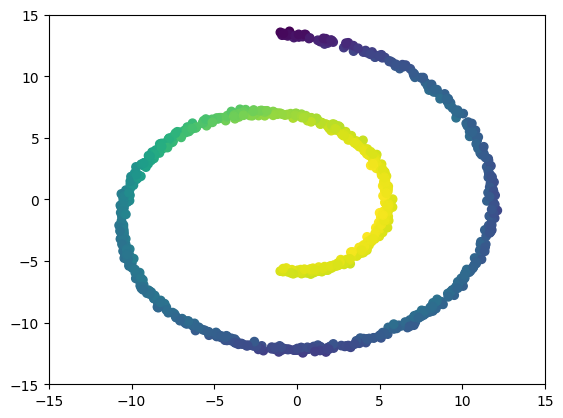



MNIST example

Dataset interpolation

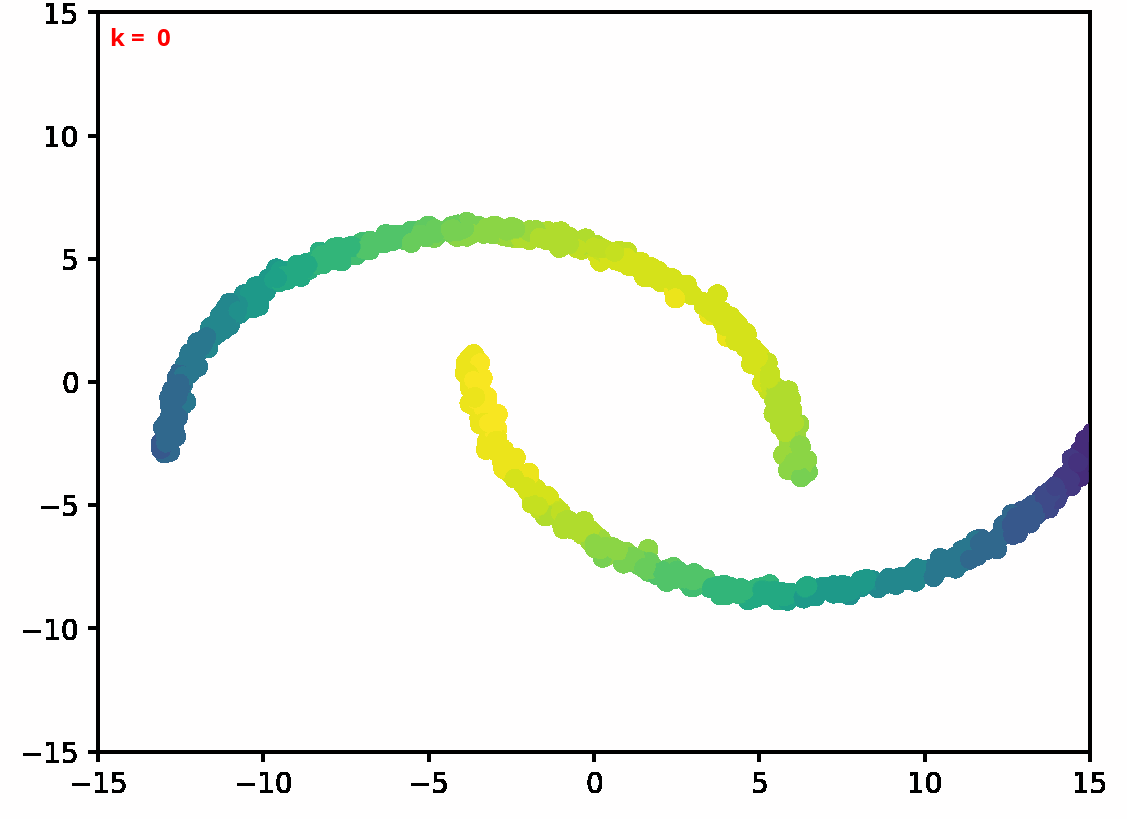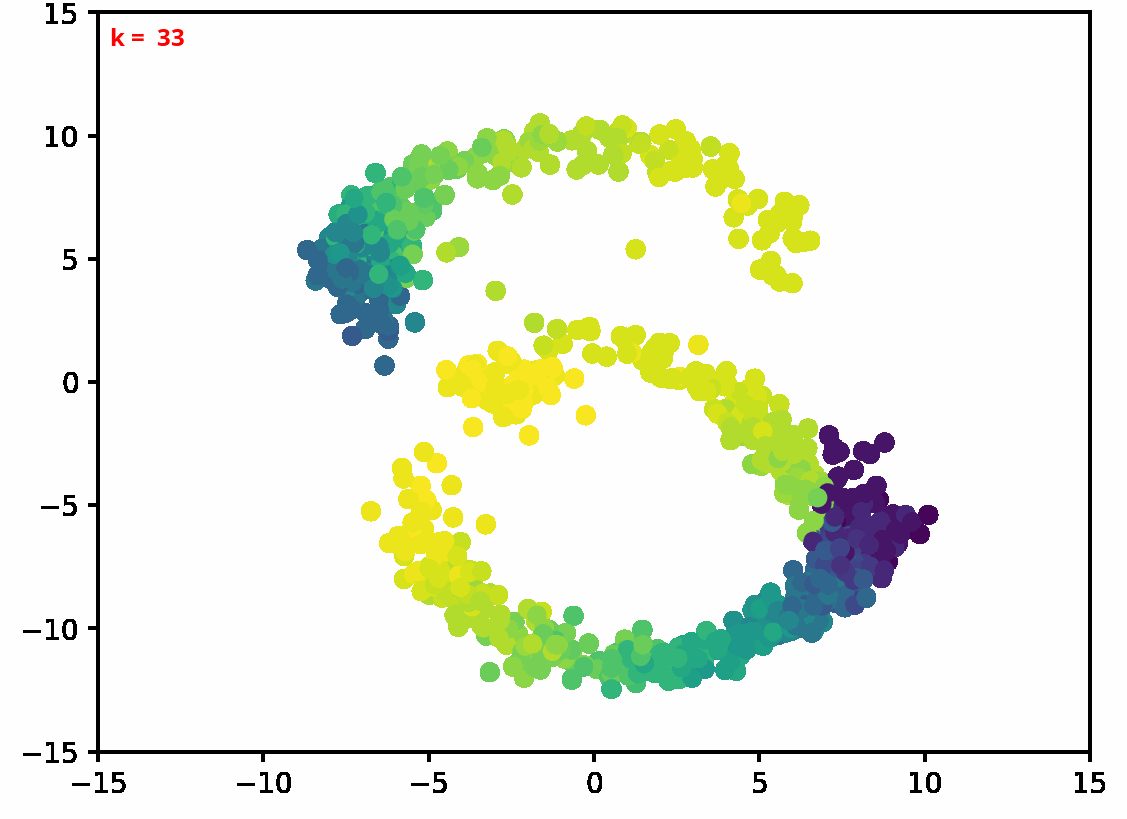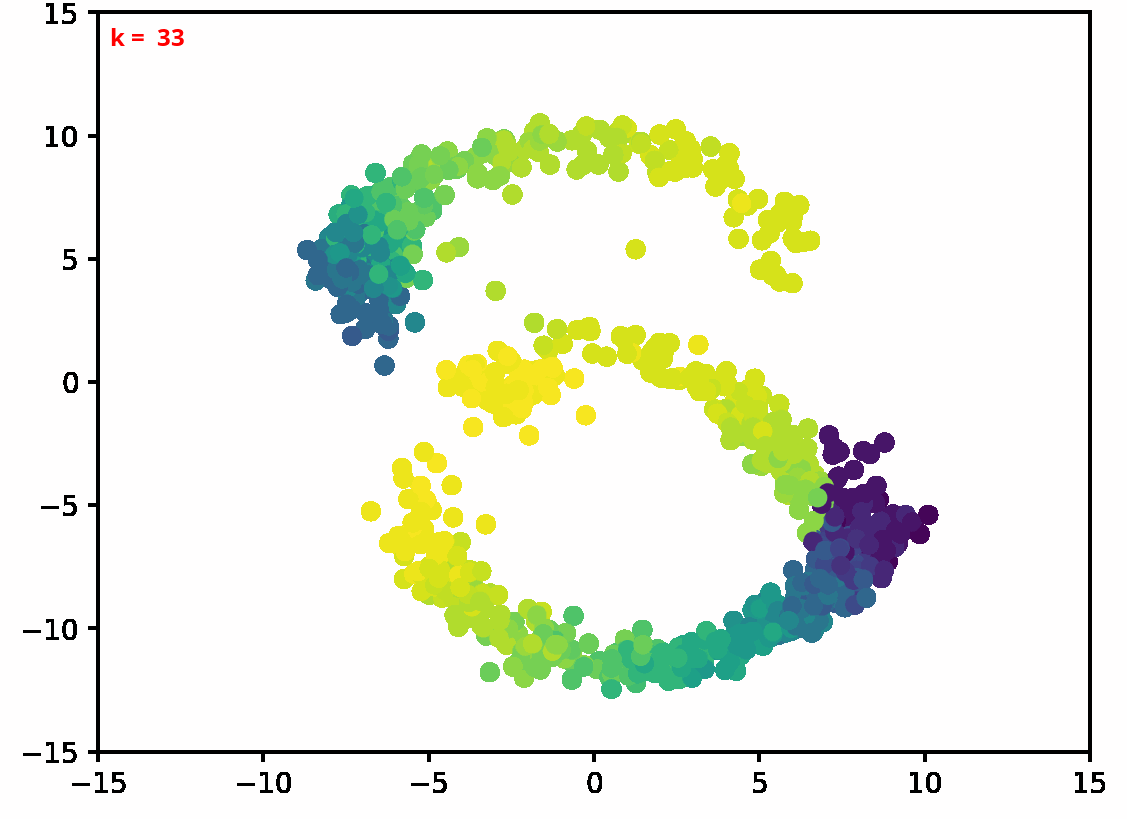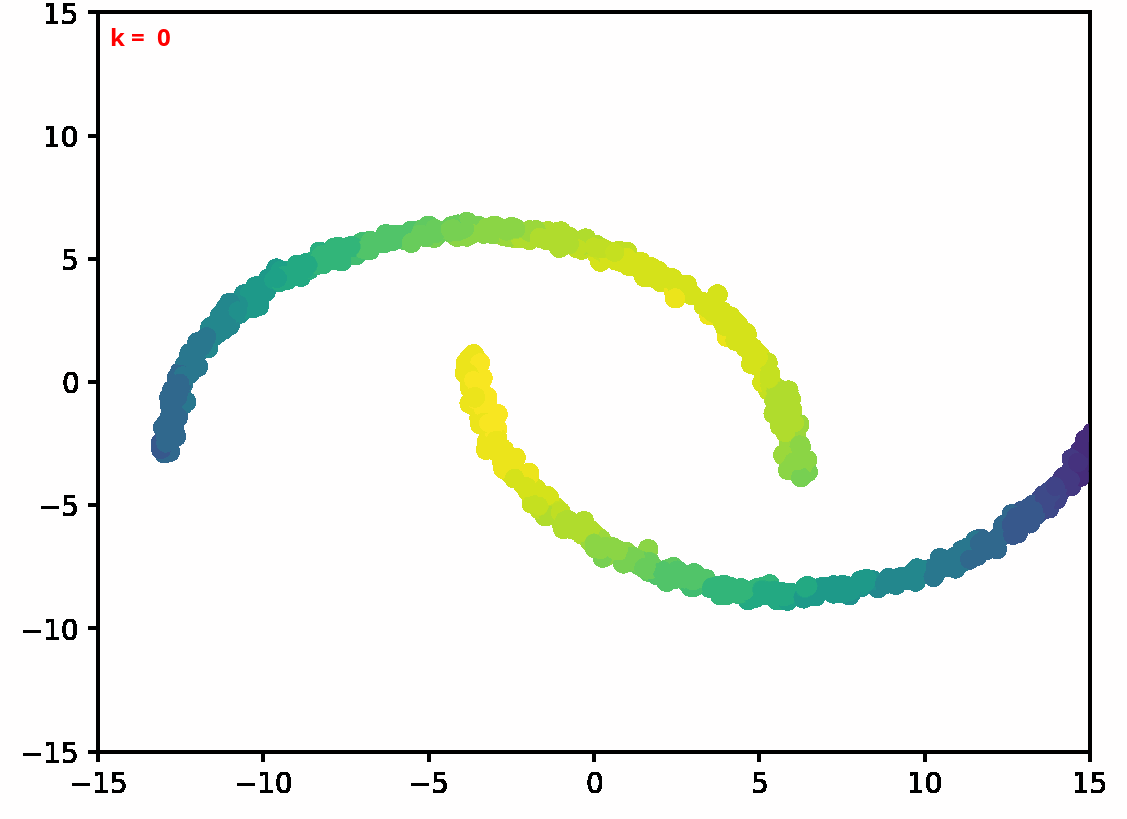


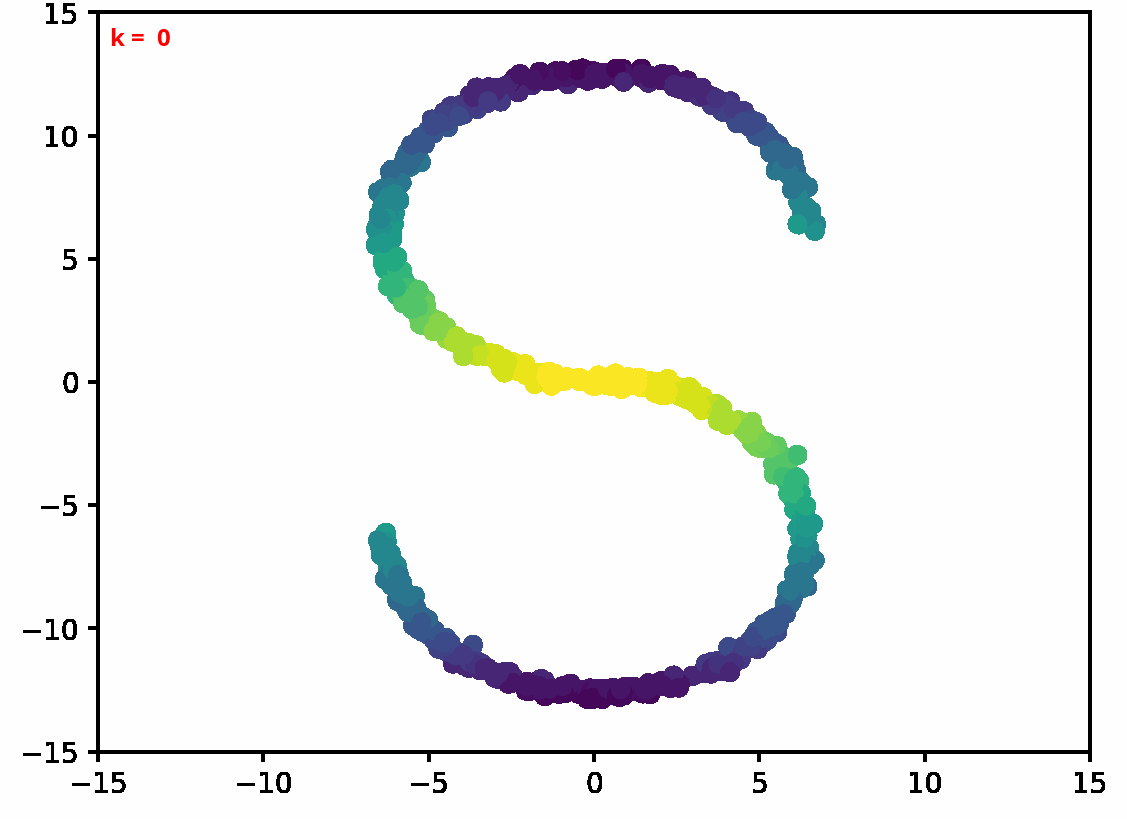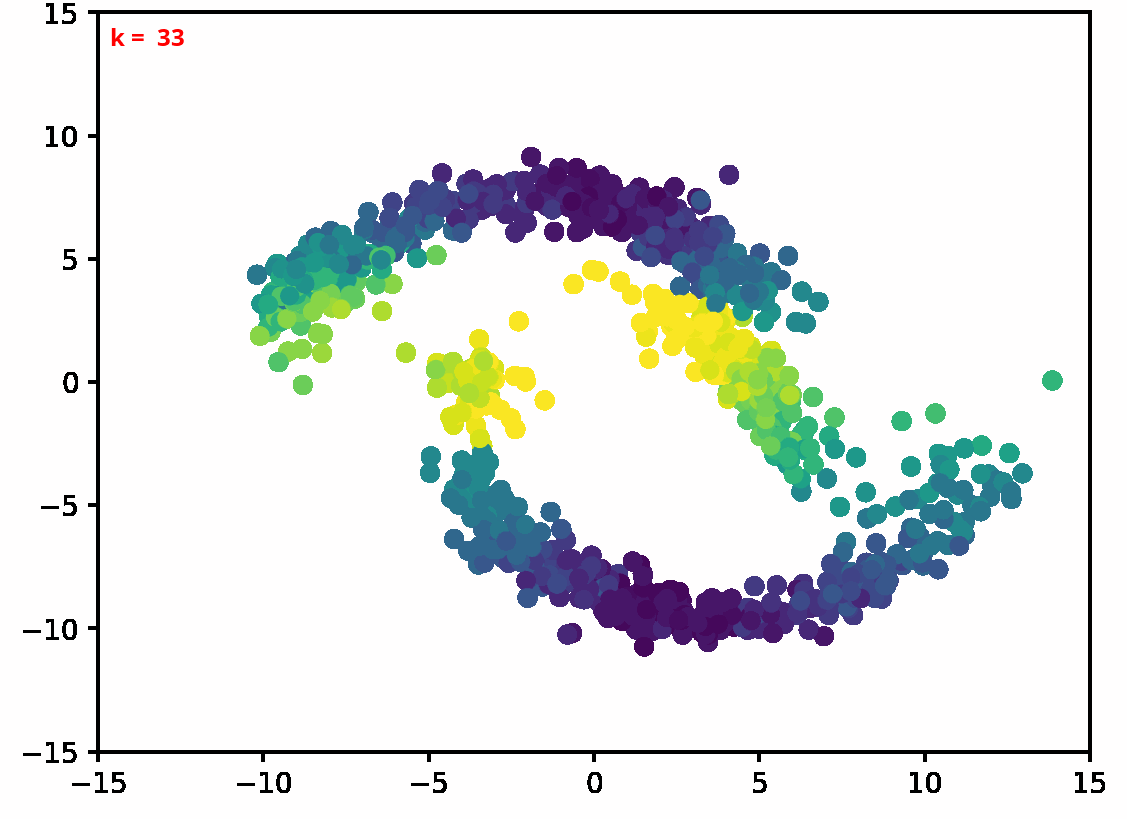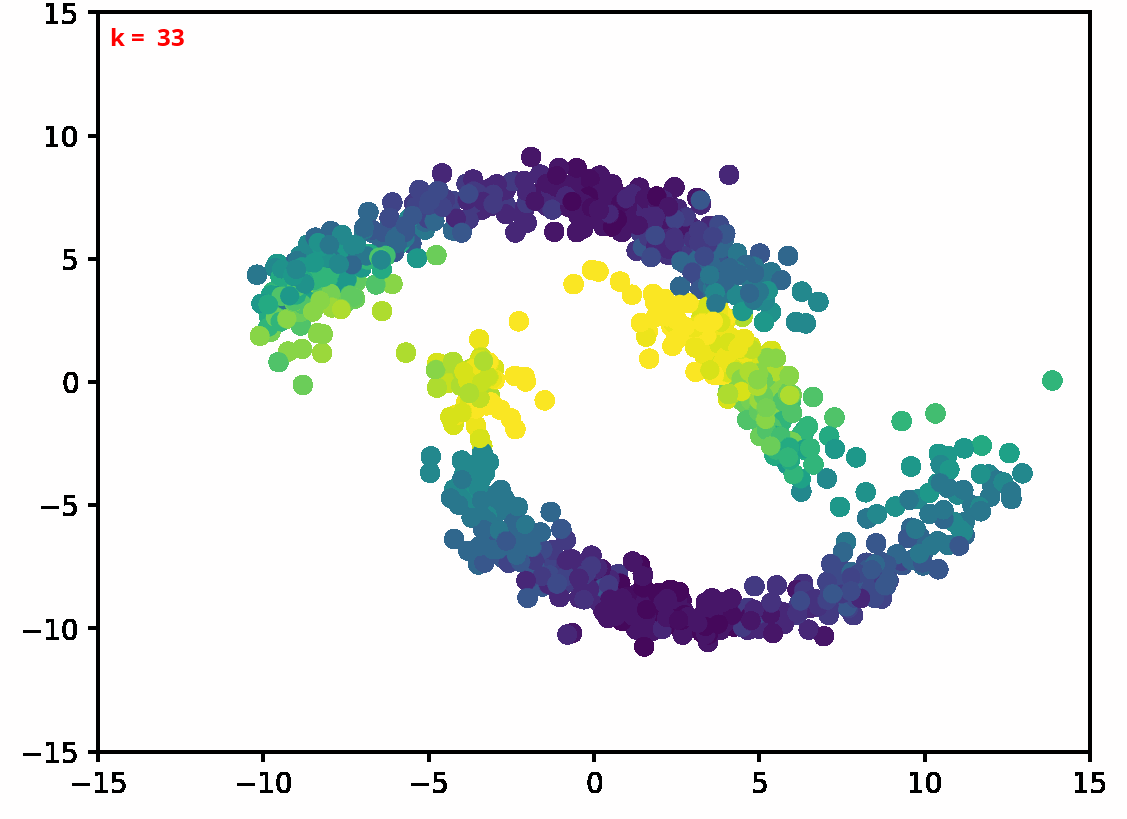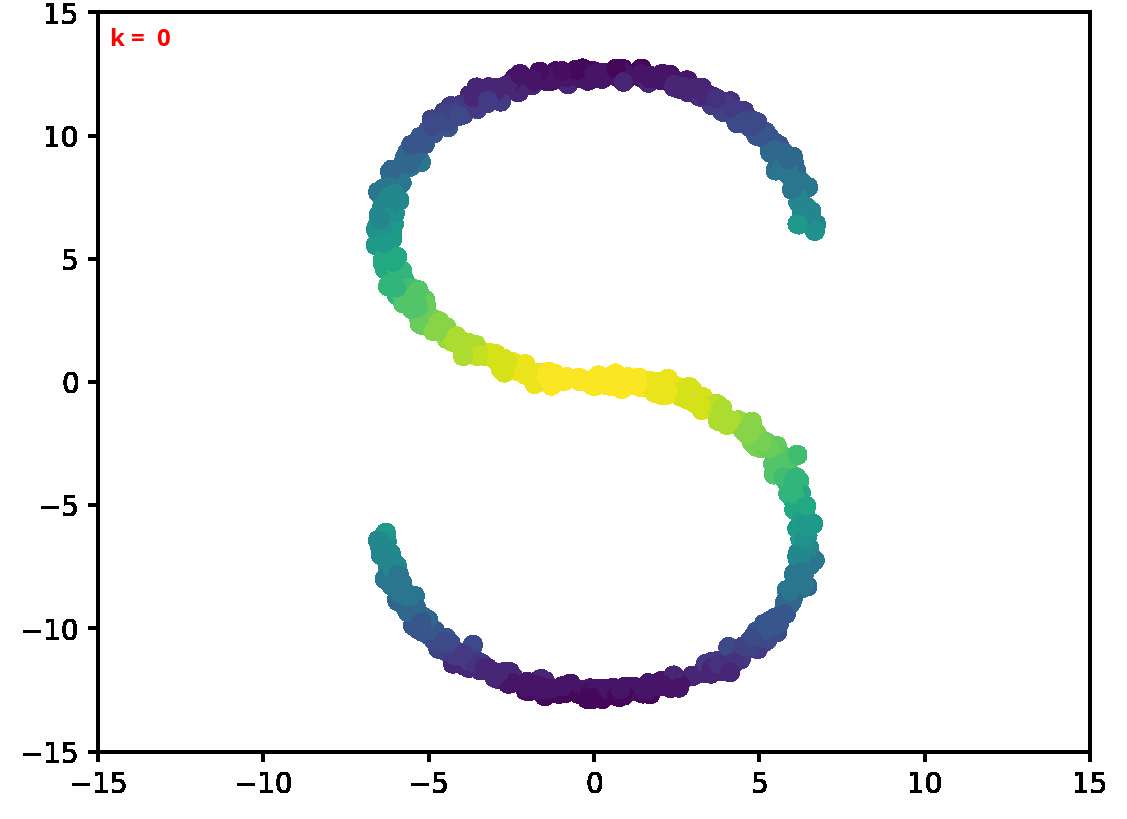



References
[1] Hans Föllmer Random fields and diffusion processes In: École d’été de Probabilités de Saint-Flour 1985-1987
[2] Christian Léonard A survey of the Schrödinger problem and some of its connections with optimal transport In: Discrete & Continuous Dynamical Systems-A 2014
[3] Yongxin Chen, Tryphon Georgiou and Michele Pavon Optimal Transport in Systems and Control In: Annual Review of Control, Robotics, and Autonomous Systems 2020
[4] Aapo Hyvärinen and Peter Dayan Estimation of non-normalized statistical models by score matching In: Journal of Machine Learning Research 2005
[5] Yang Song and Stefano Ermon Generative modeling by estimating gradients of the data distribution In: Advances in Neural Information Processing Systems 2019
[6] Jonathan Ho, Ajay Jain and Pieter Abbeel Denoising diffusion probabilistic models In: Advances in Neural Information Processing Systems 2020
